Convolutional Neural Network: How is it different from the other networks?

I am not a deep learning researcher, but I’ve come to know a few things about neural networks through various exposures. I’ve always heard that CNN is a type of neural network that’s particularly good at image-related problems. But, what does that really mean? What’s with the word “convolutional”? What’s so unusual about an image-related problem that a different network is required?

Recently I had the opportunity to work on a COVID-19 image classification problem and built a CNN-based classifier using tensorflow.kerasthat achieved an 87% accuracy rate. More importantly, I think that I’ve figured out the answers to those questions. In this post, I share with you those answers in an intuitive math-free way. If you are already familiar with DNNs and CNNs, this post should feel like a good refresher. If not, at the end of this post, you could gain an intuitive understanding of the motivation behind CNN and the unique features that define a CNN.

• Deep neural network
  • Forward propagation
  • Backpropagation
• Convolutional neural network
  • The power of convolution
  • Key features of a CNN
• What’s next?

Deep neural network

If you are familiar with DNNs, feel free to skip to Convolutional neural network. Before diving into neural networks, let’s first see the machine learning big picture:

Machine learning (ML) is the study of computer algorithms that improve automatically through experience. – Wikipedia

Looking at the problems that ML tries to solve, ML is often sliced into

• Supervised learning: predicting a label, e.g., classification, or a continuous variable;
• Unsupervised learning: pattern recognition for unlabeled data, e.g., clustering;
• Reinforcement learning: algorithms learn the best way to “behave”, e.g., AlphaGo, self-driving cars.

Among others, deep learning is a powerful form of machine learning that has garnered much attention for its successes in computer vision (e.g., image recognition), natural language processing, and beyond. The neural network is inspired by information processing and communication nodes in biological systems. By design, input data is passed through layers of the network, containing several nodes, analogous to “neurons”. The system then outputs a particular representation of the information. DNN is probably the most well-known network for deep learning, and it can be trained to learn the features of the data very well.

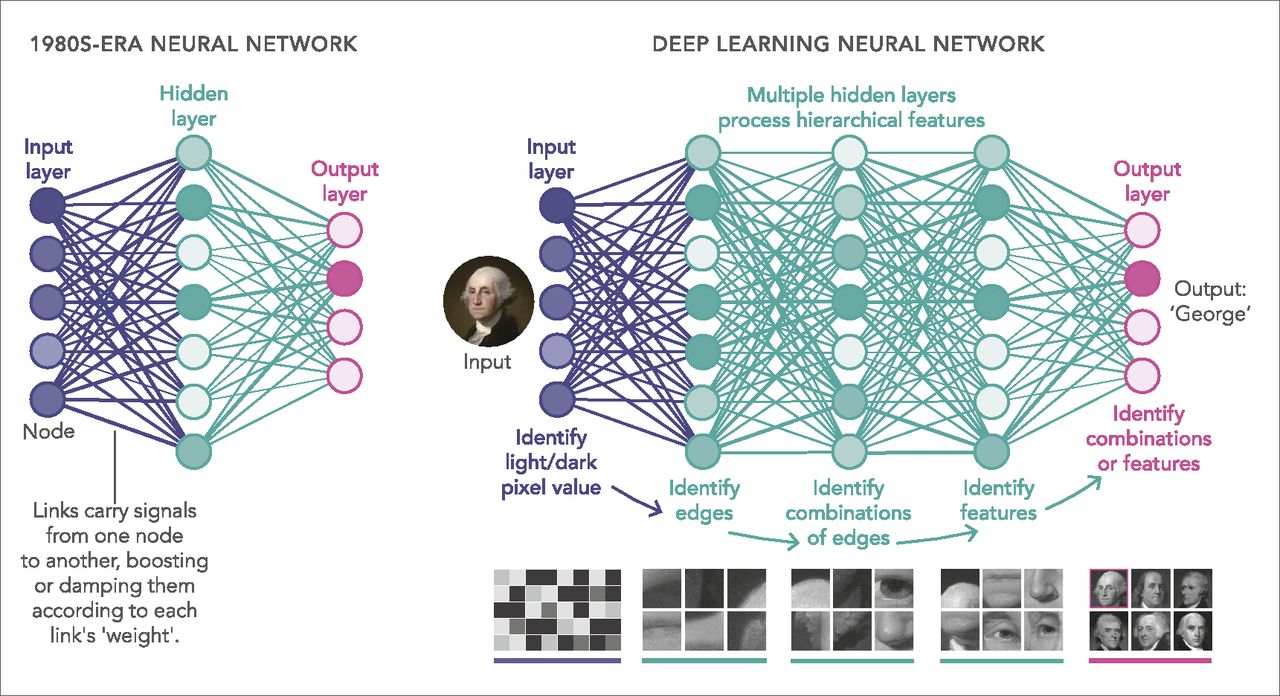Image credit.

Roughly speaking, there are two important operations that make a neural network.

1. Forward propagation
2. Backpropagation

Forward propagation

This is the prediction step. The network reads the input data, computes its values across the network, and gives a final output value.

But how does the network computes an output value? Let’s see what happens in a single layer network when it makes one prediction. It takes input as a vector of numbers. Each node in the layer has its weight. When the input value is passed through the layer, the network computes its weighted sum. This is usually followed by a (typically nonlinear) activation function, e.g., step function, where the weighted sum is “activated”.

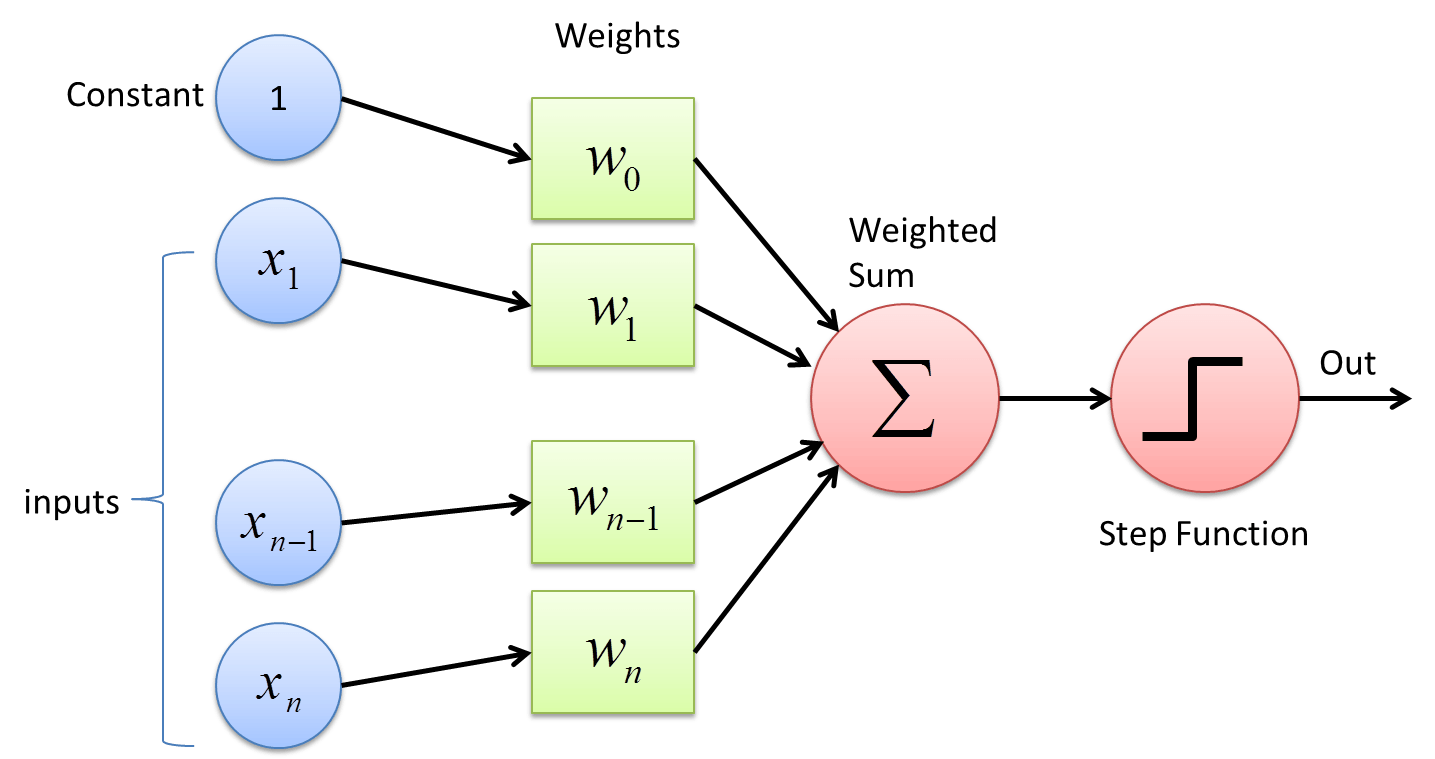Image credit.

If you know a bit about algebra, this is what the operation is doing:

where $\mathbf{w}\cdot \mathbf{x} + b$ is the weighted sum, $f(\cdot)$ is the activation function, and $y$ is the output. Now, in a deeper neural network, the procedure is essentially the same, i.e., the input –> weighted sum –> activation process is repeated for each layer.

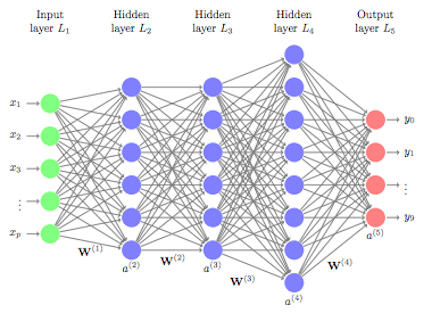Image credit.

Backpropagation

This is the training step. By comparing the network’s predictions/outputs and the ground truth values, i.e., compute loss, the network adjusts its parameters to improve the performance.

How does the network adjust the parameters (weights and biases) through training? This is done through an operation called backpropagation, or backprop. The network takes the loss and recursively calculates the loss function’s slope with respect to each parameter. Calculating these slopes requires the usage of chain rule from calculus; you can read more about it here.

An optimization algorithm is then used to update network parameters using the gradient information until the performance cannot be improved anymore. One commonly used optimizer is stochastic gradient descent.

One analogy often used to explain gradient-based optimization is hiking. Training the network to minimize loss is like getting down to the lowest point on the ground from a mountain. Backprop operation finding the loss function gradients is like finding the path on your way down. The optimization algorithm is the step where you actually take the path and eventually reach the lowest point. 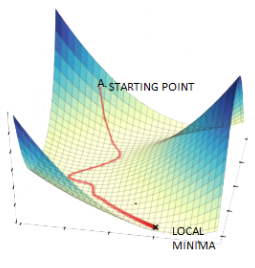Image credit.

I am glossing over many details, but I hope you now know that DNN

• is a powerful machine learning technique;
• can be used to tackle supervised, unsupervised and reinforcement learning problems;
• consists of forward propagation (input to output) and backpropagation (error to parameter update).

We are ready to talk about CNN!

Convolutional neural network

Ordinary neural networks that we’ve talked about above expect input data to be a vector of numbers, i.e., $\mathbf{x} = [x_1, x_2, x_3, \dots]$. What if we want to train an image classifier, i.e., use an image as the input? Let’s talk about some digital image basics.

• An image is a collection of pixels. For example, a 32-by-32 image has $32 \times 32 = 1024$ pixels.
• Each pixel is an intensity represented by a number in the range $[0, 255]$, $0$ is black and $255$ is white.
• Color images have three dimensions: [width, height, depth] where depth is usually 3.
• Why is depth 3? That’s because it encodes the intensity of [Red, Green, Blue], i.e., RGB values.

Therefore, this black and white Lincoln image is just a matrix of integers. Image credit.

Since a digital image can be represented as a 2D grid of pixel values, we could stretch out/flatten the grid, make it into a vector of numbers and feed it into a neural network. That solves the problem…right?

However, there are two major limitations to this approach.

1. It does not scale well to bigger images.
   • While it is still manageable for an input with $32\times32 = 1024$ dimensions, most real-life images are bigger than this.
   • For example, a color image of size 320x320x3 would translate to an input with dimension 307200!
2. It does not consider the properties of an image.
   • Locality: Nearby pixels are usually strongly correlated (e.g., see the outline of Lincoln’s face). Stretching it out breaks the pattern.
   • Translation invariance: Meaningful features could occur anywhere on an image, e.g., see the flying bird.

Image credit.

The power of convolution

On the other hand, CNN is designed to scale well with images and take advantage of these unique properties. It does with two unique features:

1. Weight sharing: All local parts of the image are processed with the same weights so that identical patterns could be detected at many locations, e.g., horizontal edges, curves and etc.
2. Hierarchy of features: Lower-level patterns learned at the start are composed to form higher-level ones across layers, e.g., edges to contours to face outline.

This is done through the operation of convolution:

1. Define a filter: a 2D weight matrix of a certain size, e.g. 3-by-3 filter.
2. Convolve the whole image with the filter: multiply each pixel under the filter with the weight.
3. Convolution output forms a new image: a feature map.
4. Using multiple filters (each with a different weight matrix), different features can be captured.

Convolution example: mean filter

Actually, let’s see the operation in numbers and images. It will be easier to understand what’s really going on. Here we create an image of a bright square using 0s and 1s. matplotlib interprets values in [0,1] the same as in [0, 255].

Original image pixel values: 
 [[0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 1. 1. 0. 0.]
 [0. 0. 1. 1. 1. 0. 0.]
 [0. 0. 1. 1. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0.]]

And this is how the image looks like:

Recall that a filter is a 2D weight matrix. Let’s create an example filter, and call it the “mean filter”:

[[0.11 0.11 0.11]
 [0.11 0.11 0.11]
 [0.11 0.11 0.11]]

In a convolution, this “mean filter” actually slides across the image, takes the values of 9 connected pixels, multiplies each with the weight (0.11), and returns the sum, i.e., the weighted average of the original 9 values, hence the name “mean filter”:

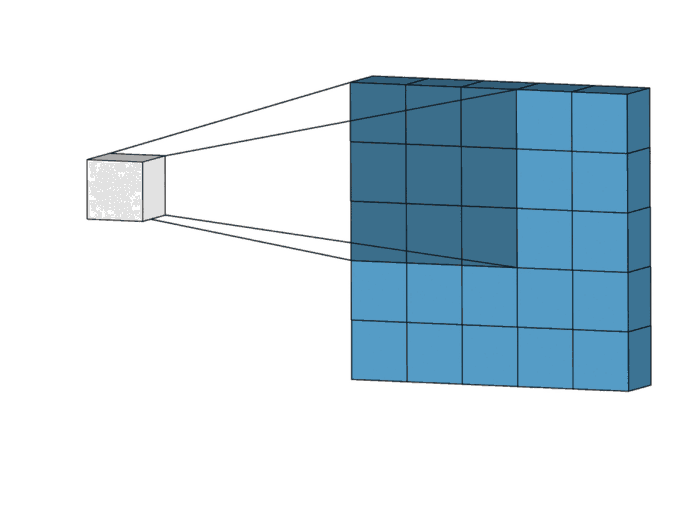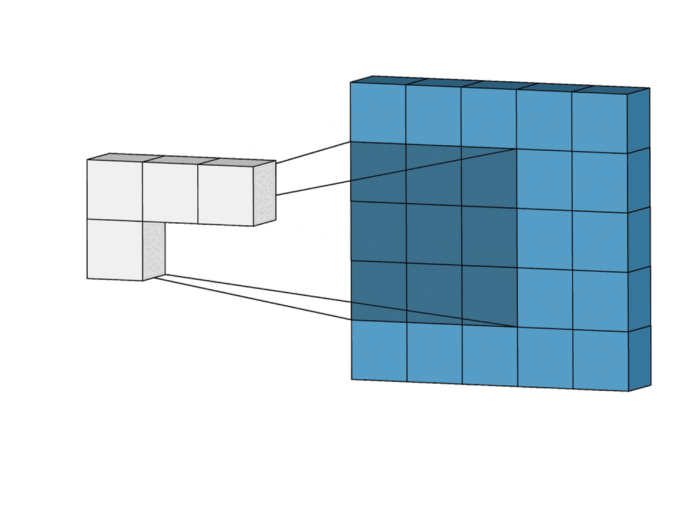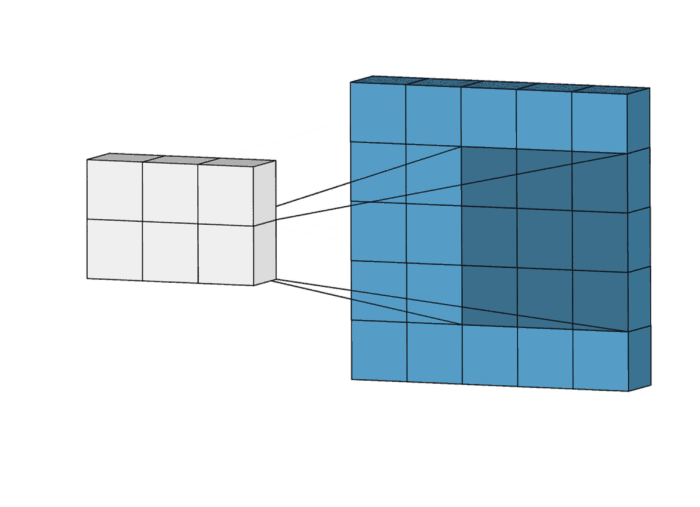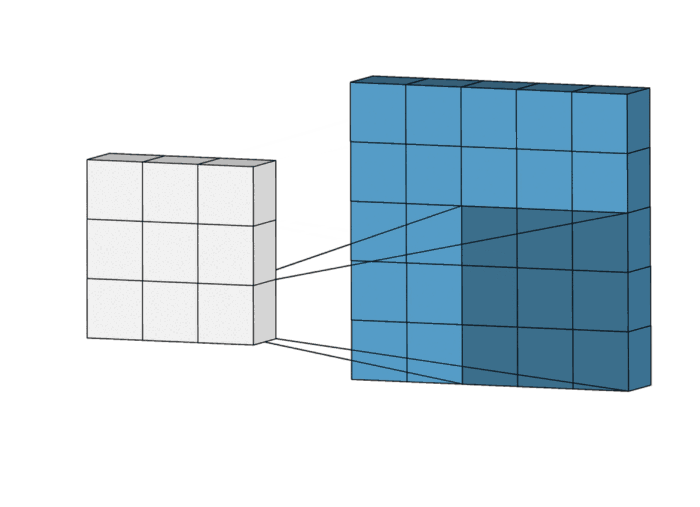
You can see the averaging effect from the filtered image pixel values. It blurs out any edges in the image.

Filtered image pixel values: 
 [[0.11 0.22 0.33 0.22 0.11]
 [0.22 0.44 0.67 0.44 0.22]
 [0.33 0.67 1.   0.67 0.33]
 [0.22 0.44 0.67 0.44 0.22]
 [0.11 0.22 0.33 0.22 0.11]]

What’s this to do with a convolutional neural network?

Well, CNN essentially applies the same convolution procedure, but the key difference is it learns the filter weights through backpropagation (training).

Also, there are usually many filters for each layer, each with a different weight matrix, applied to the same image. Each filter would capture a different pattern of the same image. A CNN could also have many layers of convolution. The complexity of the network allows features at different scales to be captured. This is the hierarchy of features mentioned above.

For example, here’s an illustration of features learned by filters from early to the latter part of the network.

• Early filters capture edges and textures. (General)
• Latter filters form parts and objects. (Specific)

Image credit.

Key features of a CNN

While DNN uses many fully-connected layers, CNN contains mostly convolutional layers. In its simplest form, CNN is a network with a set of layers that transform an image to a set of class probabilities. Some of the most popular types of layers are:

• Convolutional layer (CONV): Image undergoes a convolution with filters.
• RELU layer (RELU): Element-wise nonlinear activation function (same as those in DNN before).
• Pooling layer (POOL): Image undergoes a convolution with a mean (or max) filter, so it’s down-sampled.
• Fully-connected layer (FC): Usually used as the last layer to output a class probability prediction.

Now, if you are designing your own CNN, there are many elements to play with. They generally fall into two categories:

1. Type of convolutional layer
   • Depth: The number of filters to use for each layer.
   • Stride: How big of a step to take when sliding the filter across the image, usually 1 (see the convolution GIF above) or 2.
   • Size: Size of each convolution filter, e.g., the mean filter is 3-by-3.
   • Padding: Whether to use paddings around images when doing convolution. This determines the output image size.
   • And others.
2. How to connect each layer?
   • Besides the type of layers, you need to design an architecture for your CNN. This is an active field of research, e.g., what’s a better architecture? or can we automatically search for a better architecture? Check “neural architecture search” out if you are interested.
   • A commonly used architecture goes like this:
     • $\text{INPUT} \rightarrow [ [\text{CONV} \rightarrow \text{RELU}]^N \rightarrow \text{POOL}]^M \rightarrow [\text{FC} \rightarrow \text{RELU}]^K \rightarrow \text{FC}$
     • The power $N, M, K$ means that the operation is repeated those number of times.

What’s next?

Thank you for reading until the end! I hope by now you could see the difference between a CNN and a regular DNN, and also gained an intuitive understanding of what convolution operation is all about. Please let me know your thoughts or any feedback in the comment section below.

In the next article, we explore how CNN can be used to build a COVID-19 CT scan image classifier. Unsurprisingly, a pre-trained CNN can achieve strong baseline performance (85% accuracy). However, it would take more than a neural network to produce reliable and convincing results. Here’s the article:
What deep learning needs for better COVID-19 detection

Further resources

If you are interested in knowing more about CNNs, check out 👉:

• CS231n Convolutional Neural Networks for Visual Recognition
• DeepMind x UCL | Convolutional Neural Networks for Image Recognition

and how to implement them 👉:

• Introduction to Keras for Engineers
• Tensorflow Keras CNN Guide

Enjoy! 👏👏👏